７．トポロジカル量子計算

トポロジカル量子計算を説明する前にまず、トポロジカル量子メモリを説明しないといけません。トポロジカル量子メモリは以下のように定義されます。

Surface codeとかToric codeとか系のジオメトリー（トポロジー）に応じて呼びわけられます。

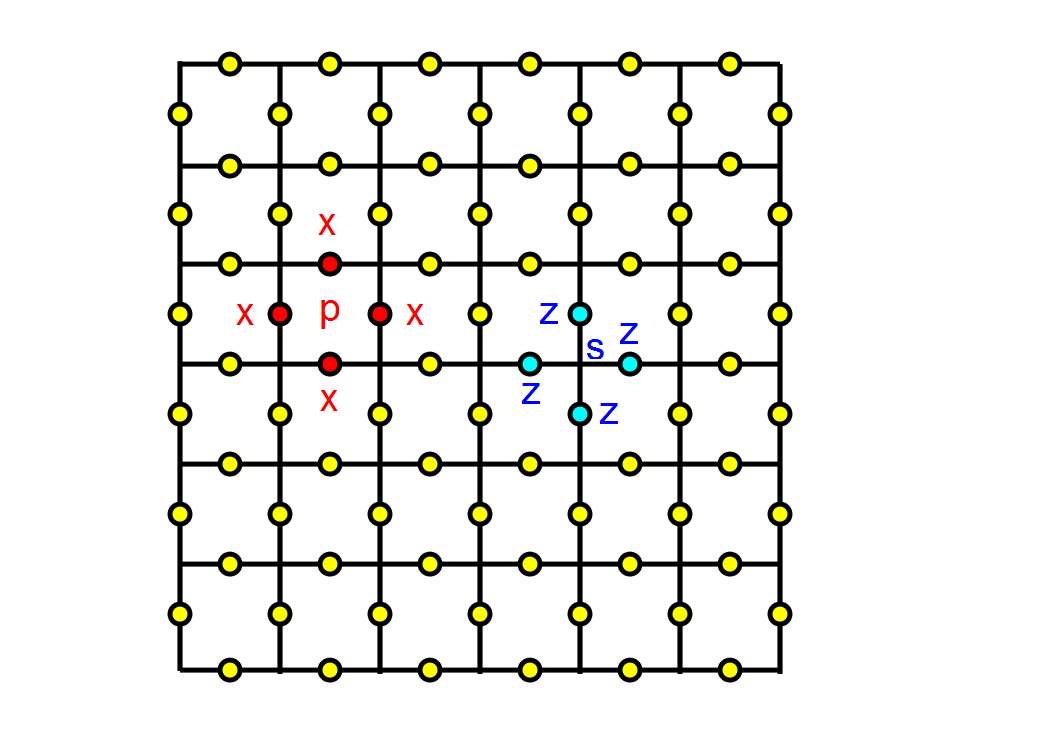
２次元トーラス上の、平方格子を考えます。（トーラスなので、Toric codeです。）

頂点ではなく、辺にキュービットが乗っています。（黄色いつぶつぶがキュービットです。）

で、Toric codeは、互いに可換な演算子たち

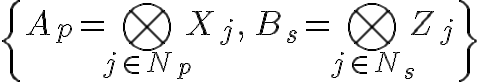
の同時固有状態として定義されます。ここで、ｐというのは、上の図のような、ある、

四角（プラケット）で、ｓというのは、上の図のような十字（スター）です。

N_pというのは、一つのプラケットに含まれるキュービットの集合、N_sというのは一つのスターに

含まれるキュービットの集合です。

すぐに分かるように、これらの演算子はすべて可換なので、同時固有ベクトルが定義できます。

簡単な練習問題ですが、下のように、ちぢめると１点に集約できるような閉じたループの形に

X,Zをかけても、状態は不変です。（Xは格子上でのループ。ZはDual格子上でのループ。）

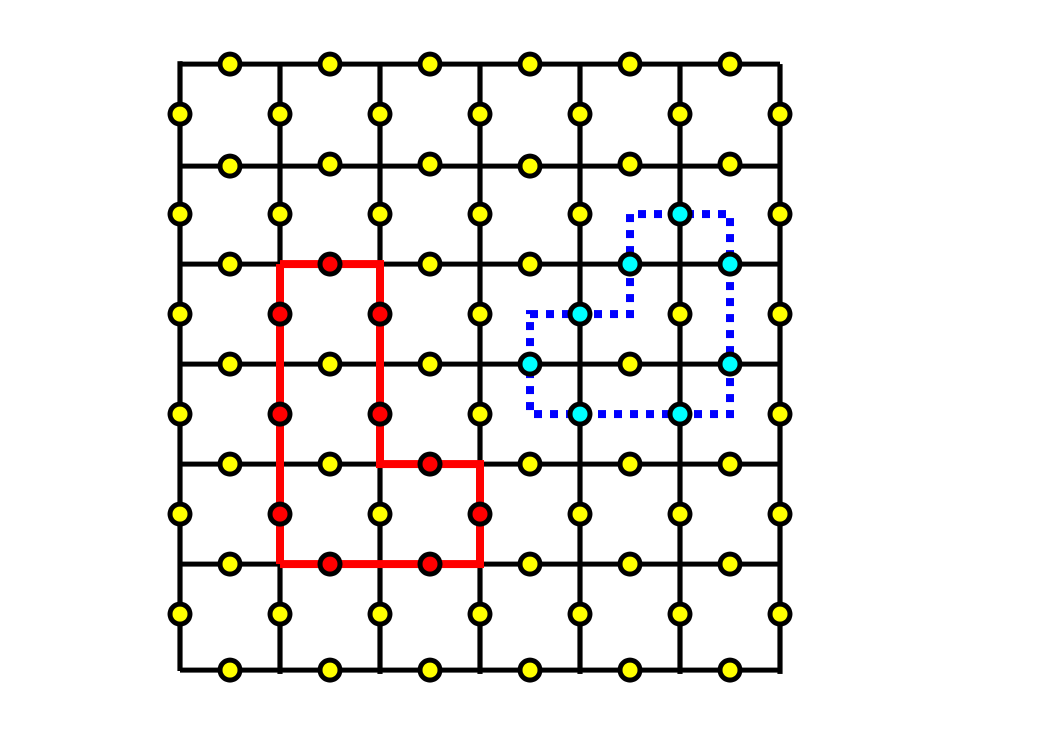
ところが、これも簡単に確かめれるように、下の図のように、いわゆる、トポロジー的に非自明な

ループ（ちぢめても、１点に集約できない）でXをかけると、状態は直行する状態に移ります。

つまり、ハミルトニアン

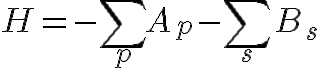
を考えたとき、基底状態が４重縮退していて、各基底状態が、トポロジー的に非自明なXループで

指定されるのです。４重縮退した基底状態は４次元ヒルベルト空間を張りますから、

２キュービットエンコードできることになります。つまり、Toric codeは２つのロジカルキュービットを

エンコードできるのです。そうすると、何個のロジカルキュービットをエンコードできるか、というのは、

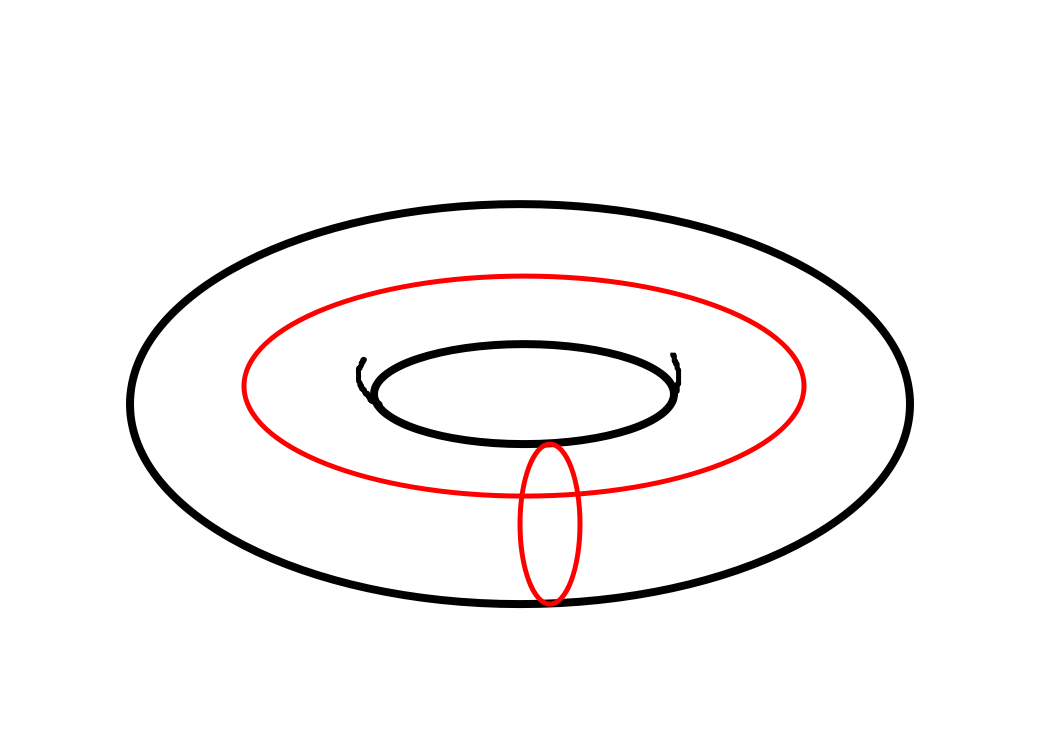
系の種数（genus）によってきまるということが分かります。たとえば、二つ穴のドーナツ

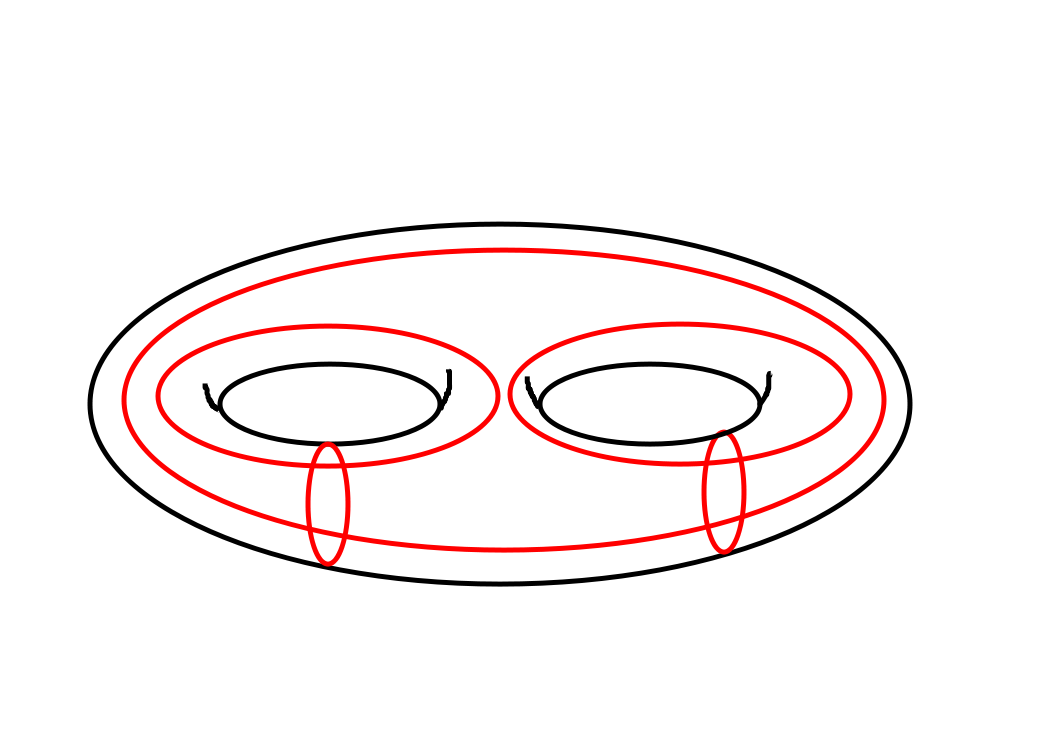
だと、非自明ループが、５個なので、５個のロジカルキュービットをエンコードできます。

さて、なぜ、これらがメモリーとして働くかというと、まず、上でみたように、一点に集約できるような

閉じたループのエラーがおきても、それはエラーとなりません。なぜなら状態が変わらないので。

状態を変えるには、上で見たように、トポロジー的に非自明な、つまりドーナツの縦か横を一周する

ようなエラーをかけないといけませんが、そんなNon-localなエラーがおきる確率は低いです。

もし、閉じたループでなくて、開いたストリング的なエラーが起こった場合、状態は変わってしまいます

が、そのようなエラーは検出できます。どうやって検出するかというと、下の図のように、

閉じたループの端っこのところのAかBを測ると、固有値が＋１ではなく、−１になっているので、

それにより検出できるのです。これだと、エラーストリングの端しか検出できないじゃないか、とおもう

かもしれませんが、上で見たように、閉じたループは、どのようにぐにぐに動かしてもいいので、

端さえ固定すれば、その間でストリングがどういう形になっているのか、というのは問題ではありません。

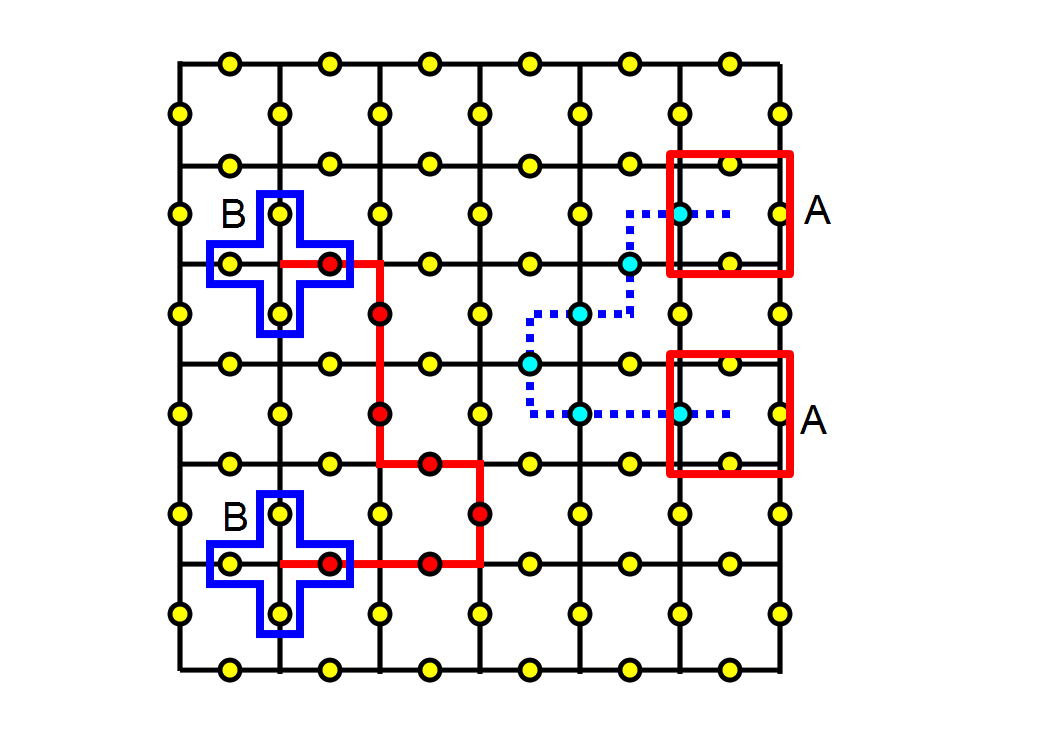
さて、このように、開いたループ状のエラーを作用させると、その端のところで、AかBの固有値が

逆転する、ということは、物性的な見方をすると、次のようです。まず、開いたループ状のエラーを

作用させるまえのToric codeは真空です。で、開いたループ状のエラーを作用させると、

開いたループの端のところに粒子が発生し、系が真空から、低エネルギー励起状態になります。

この粒子は、ストリングで結ばれており、常にペアーでつくられるのです。

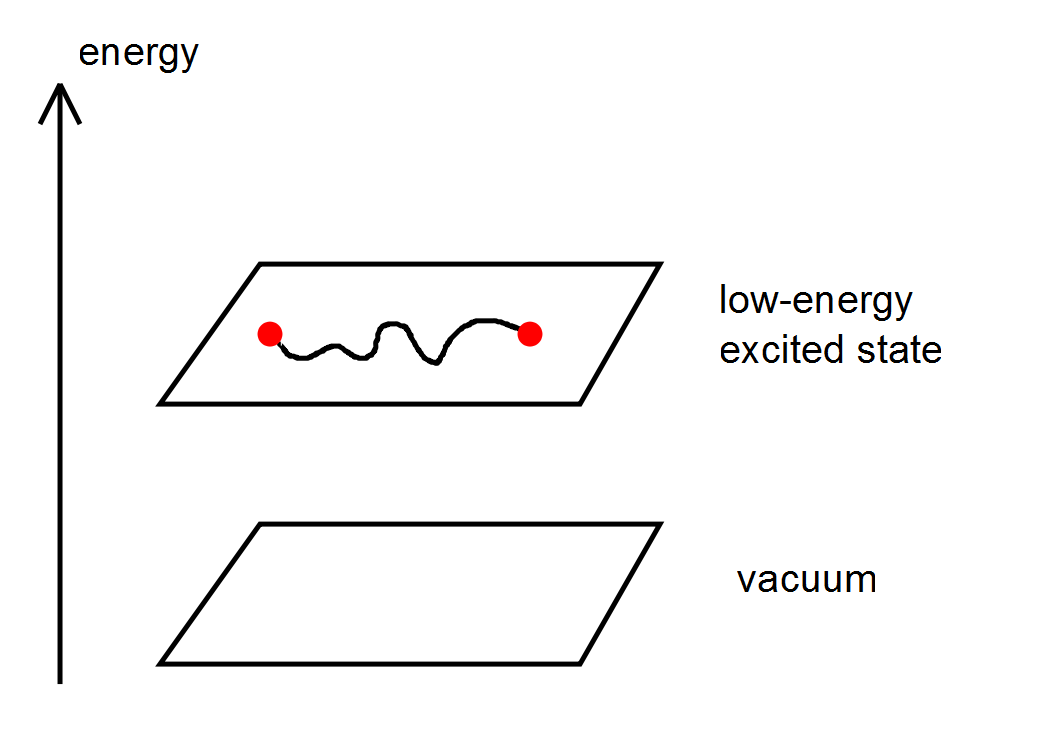
そして、この粒子は、ボソンでも、フェルミオンでもなくて、エニオンというものなのです。

ボソンは２つの粒子の位置を交換してもなにもおこらないが、フェルミオンは２つの粒子の

位置を交換するとマイナス符号がつきます。エニオンはもっと複雑なことがおこります。

（Abelian anyonだと、exp(iθ)というU(1) Phaseがつき、Non-abelianだと、もっと複雑な非可換

ユニタリがおこります。）

さて、実際に、Toric codeの素励起がエニオンであることを確認しましょう。（準備中）

さて、このように、エニオンをまわすと、ある意味量子ゲートができることがわかりました。では、

エニオンをいっぱい用意して、ぐりぐり交差させれば、量子計算ができてしまうのではないか！

と思えます。エニオンがどう交差するか、というところしか問題でないので、エニオンの軌跡をこまかく

制御しなくてもいいわけです。これは、あるいみ、トポロジーで守られた、ロバストさといえます！

しかし、残念なことに、Abelianエニオンの場合、ぐりぐりまわしても、クリフォードゲートしかできません。

（Non-abelianの場合は、Universalな量子ゲートができる例が知られています。）

クリフォードゲートだけでは量子計算ができないので、クリフォードでないようなゲートも必要です。

では、クリフォードで無いゲートはどうやって実現すればいいのでしょうか？

実は、Magic state と呼ばれる、特別な状態を用意しさえすれば、いいのです[S. Bravyi and A. Kitaev, PRA71, 022316(2005)]。

下のような回路を考えましょう。

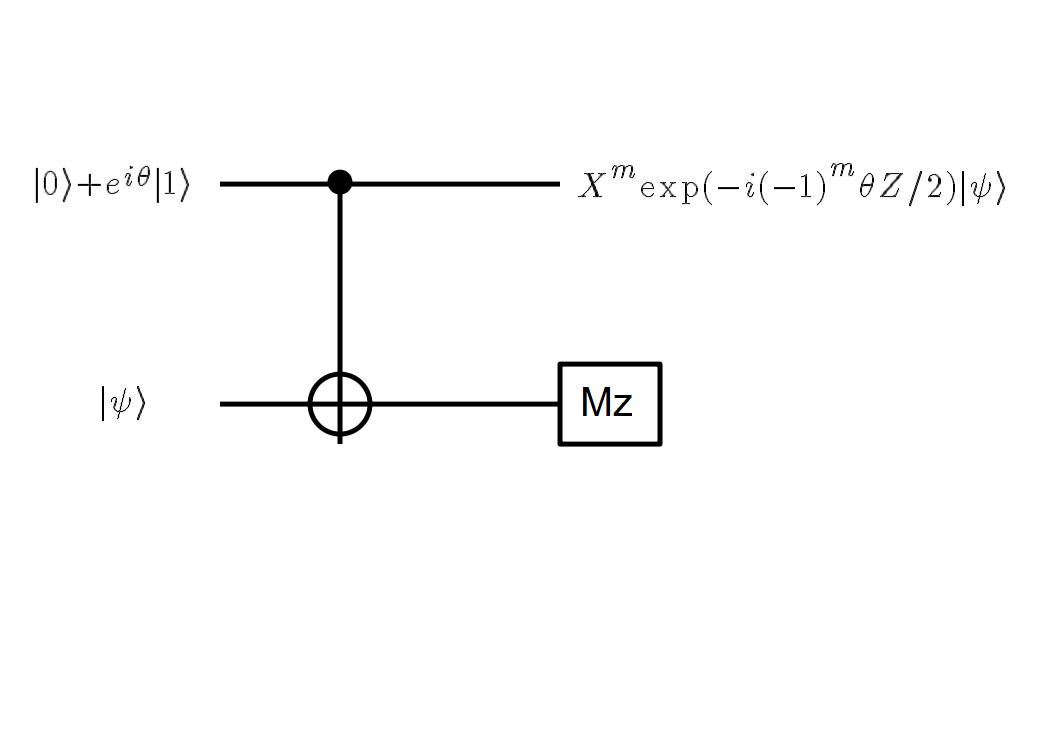
つまり、|0>+exp(iθ)|1>が用意できれば、ｚ回転exp(-iθZ/2)がC-NOTとZ基底測定、

つまりクリフォードだけで実現できるのです。例えば、θ＝-π/4とすれば、ノンクリフォードである

exp(iθZ/8)が実現できます。しかし、そのような状態をつくるのはノイズフリーにはできませんから、

できた状態にはエラーがかかってしまいます。ところが、Magic stateと呼ばれる特殊な状態たちは、

クリフォードゲートのみを使用して、Distillationできるのです。（つまり、エラーのある不完全な

Magic stateを多く用意して、クリフォードゲートをかけると、一つのエラーのない完全な

Magic stateが、抽出、Distillationされる。）クリフォードゲートはトポロジカルにエラーフリーで

できますから、最初のMagic stateがあまりにもひどく壊れていなければ、エラーフリーで完全な

Magic stateを得ることができるのです。これを、Magic state distillationといいます。

さて、ここまでをまとめると、クリフォードゲートは、トポロジカルメモリ上に励起されたエニオンをぐりぐり

交差させて実行し、ノンクリフォードゲートはMagic stateを手でいれてdistillationする、ということでした。

しかし、これらをやるには、２キュービット以上同時にアクセスするような操作が必要です。しかし、

これらを３次元グラフ状態でシミレートすれば、すべて１粒子測定のみで可能となるのです。

[R. Raussendorf and J. Harrington, PRL98, 190504 (2007); R. Raussendorf, J. Harrington, and K. Goyal, NJP 9, 199 (2007); A. G. Fowler and K. Goyal, Quant. Info. Comput. 9, 721-738 (2009); A. G. Fowler, A. M. Stephens, and P. Groszkowski, PRA 80, 052312 (2009)]

ちいさなサイズでこれは実験的に実現されました[Gao et al. arXiv:0905.1542; accepted by Nature]。

つまり、３次元グラフ状態さえつくってしまえば、こっちのもの、あとはトポロジカル量子計算できる！

ということになったわけですが、３次元グラフ状態というのをどうやってつくれば

いいのでしょう？光学系でしたら、以前述べたようなFusionゲートを使ってつくることができます。

その際に、粒子がロスしたり、CZゲートが確率的に失敗したりするわけですが、

そこをちゃんと考えてエラーThresholdを出したのが、[S. D. Barrett and T. M. Stace, PRL 105, 200502 (2010); K. Fujii and Y. Tokunaga, PRL 105 250503 (2010); Y. Li, S. D. Barrett, T. M. Stace, S. C. Benjamin, PRL105, 250502(2010)]です。

では、光学系ではなくて、例えば、物性系、でつくろうと思ったときはどうしましょう。グラフ状態は、

スピン1/2の２体Nearest-neighbour相互作用ハミルトニアンのギャップのあるユニークな

基底状態にはなりえないという結果があるのでした。さあ困った。

ところが最近、[Y. Li, D. E. Browne, L. C. Kwek, R. Raussendorf, T. C. Wei, PRL107, 060501 (2011)]において、

スピン２とスピン3/2の２体Nearest-neighbour相互作用のギャップのあるハミルトニアンHの、

低温の熱平衡状態exp(-H/T)が、１粒子測定により、エラーのある３次元グラフ状態に変形

できることがわかりました。このエラーは温度Tが十分小さければ、量子エラー訂正で訂正できる

程度のものなので、トポロジカル量子計算が十分遂行可能です。つまり、彼らの結果は、ある、

スピン２とスピン3/2の２体Nearest-neighbour相互作用のギャップのあるハミルトニアンを用意して、

それを十分低温の熱平衡状態にしさえすれば、トポロジカル量子計算できます、

といっているわけです。

ところが、彼らの論文の直後に、スピン２とスピン3/2のハイブリッド系を考えなくても、

スピン3/2だけでOKだ、ということをが示されました。[K. Fujii and TM, PRA 85, 010304(R) (2012); arXiv:1111.0919]。

参考文献：

R. Raussendorf and J. Harrington, PRL98, 190504 (2007); 　３次元クラスター状態上でのトポロジカル量子計算の提唱

R. Raussendorf, J. Harrington, and K. Goyal, NJP 9, 199 (2007); 　それのFull paper

A. G. Fowler and K. Goyal, Quant. Info. Comput. 9, 721-738 (2009); 解説

A. G. Fowler, A. M. Stephens, and P. Groszkowski, PRA 80, 052312 (2009); 解説

S. D. Barrett and T. M. Stace, PRL 105, 200502 (2010); Particle lossを考えたThresholdの計算

K. Fujii and Y. Tokunaga, PRL 105 250503 (2010); 確率的CZゲートを考えたThresholdの計算

Y. Li, S. D. Barrett, T. M. Stace, S. C. Benjamin, PRL105, 250502(2010); 確率的CZゲートを考えたThresholdの計算

Y. Li, D. E. Browne, L. C. Kwek, R. Raussendorf, T. C. Wei, PRL107, 060501 (2011)　スピン２とスピン3/2粒子による熱平衡状態でのトポロジカル量子計算

K. Fujii and TM, PRA 85, 010304(R) (2012); arXiv:1111.0919　スピン3/2粒子のみによる熱平衡状態でのトポロジカル量子計算