Jones多項式と量子計算

Jones多項式

Jones多項式というのは、絡み合った紐（リンク）の不変量です。つまり、紐を切ることなく動かして、おなじ形になるものは同じ多項式になります。

このJones多項式はDNAとか統計物理でも重要な働きをしています。

リンクLのJones多項式V_L(t)は次のようにして定義されます。

ここで、w(L)は writhe と呼ばれる量で、リンクLに対し、向きをつけて、各交差点に下の図のように

＋１か−１を割り当てて、全ての交差点に対して足したものです。

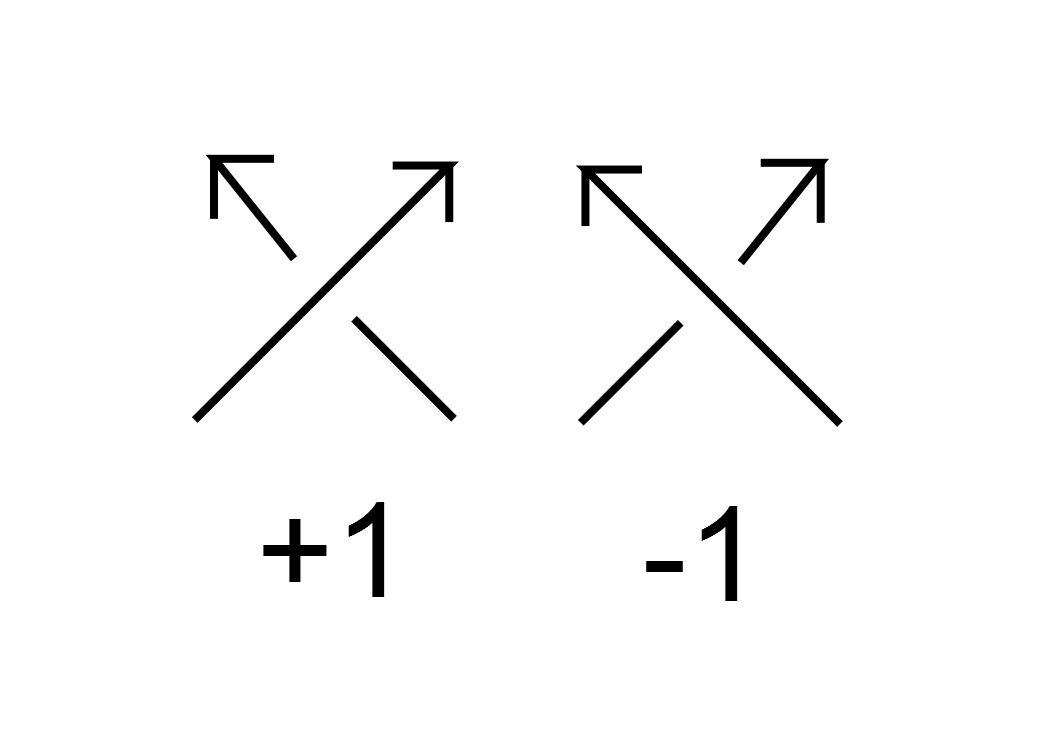
また、<L>はKauffman bracketと呼ばれるもので、

次のようにして定義されます。与えられたリンクに対し、各交差点を下の図のように変えます。

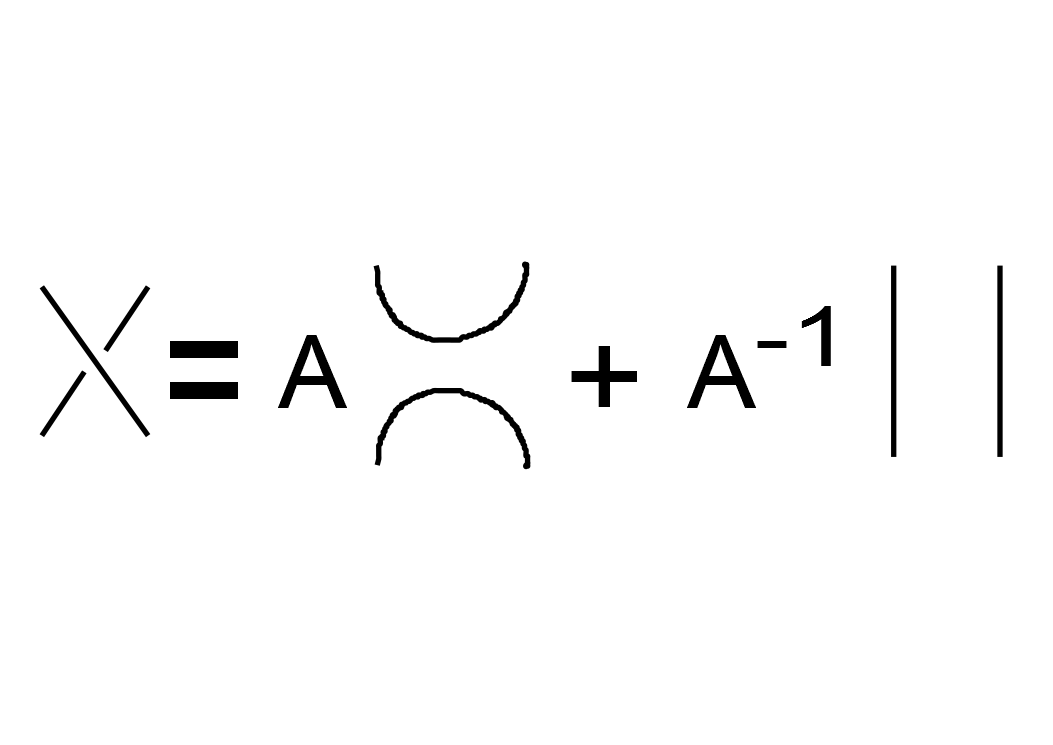
すると、2^{交差点の数}個のリンクの和になります。それらの各リンクを、d^{loopの数-1}に変えます。

そうして得られたAの多項式が<L>です。

Jones多項式の計算は#P-hardであることが知られています。

Braid群

n-strand Braidというのは、n本の糸がからみあったものです。（下図は5-Strand braidの例）

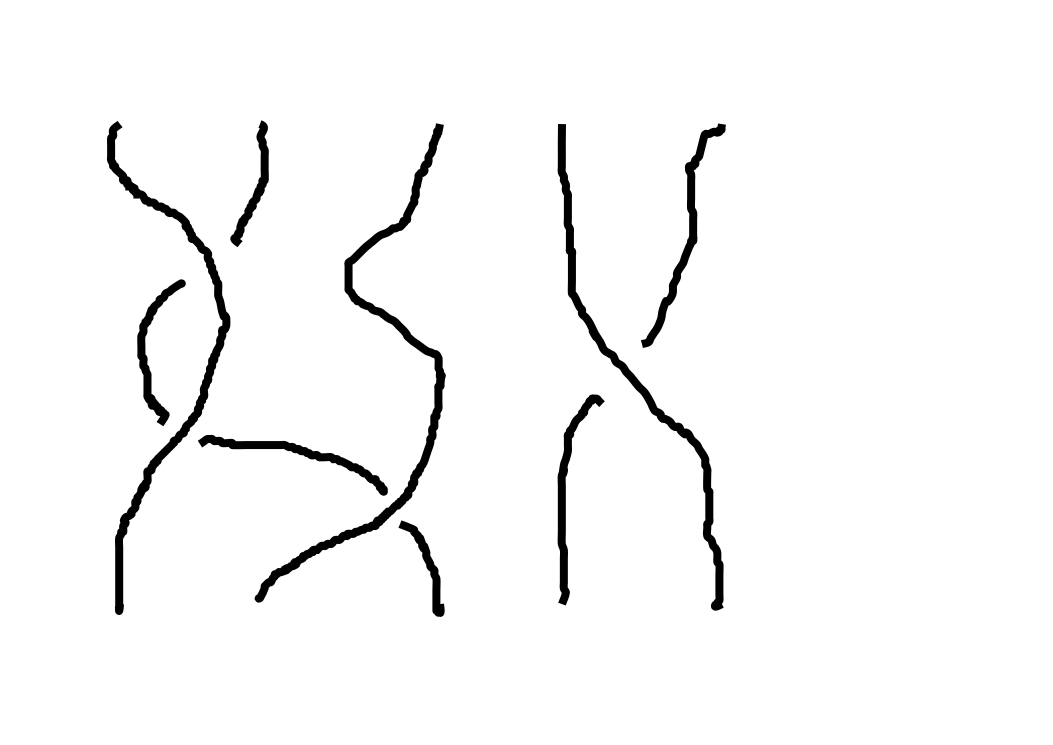
Braidの積を「Braidを縦にならべてStringをつなぐ」と定義すると、群をつくり、その群は以下の要素で生成されます（Artin presentation）。

b_i b_j = b_j b_i (|i-j|>=2)

b_i b_{i+1} b_i = b_{i+1} b_i b_{i+1}

ここで、b_iは、i番目のStrandとi+１番目のStrandが交差した状態を表します。

Braidを閉じれば、Linkができます。

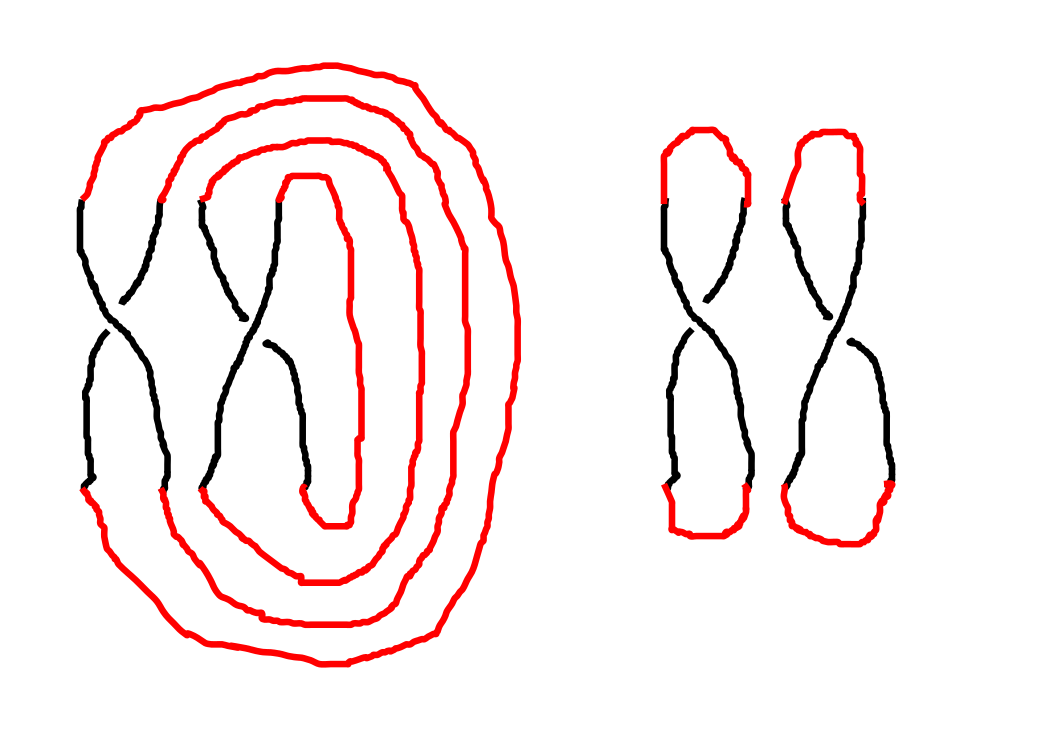
左のような閉じ方をtrace closure、右のような閉じ方をplat closureといいます。

Alexanderによると、どんなリンク もあるbraidのclosureになっており、しかもそのようなbraid は多項式アルゴリズムでみつけることが可能です。

Closureを指定すれば、Braidに対してもJones多項式が定義できます。

Temperley–Lieb algebra

Temperley–Lieb algebra TL_n(d) は次のようにして定義されます。

E_i E_j = E_j E_i (|i-j|>=2)

E_i E_{i±1} E_i = E_i

E_i^2 = d E_i

ただし、積は下の図のように定義され、（つまり、縦につんで、輪ができたらｄにする）

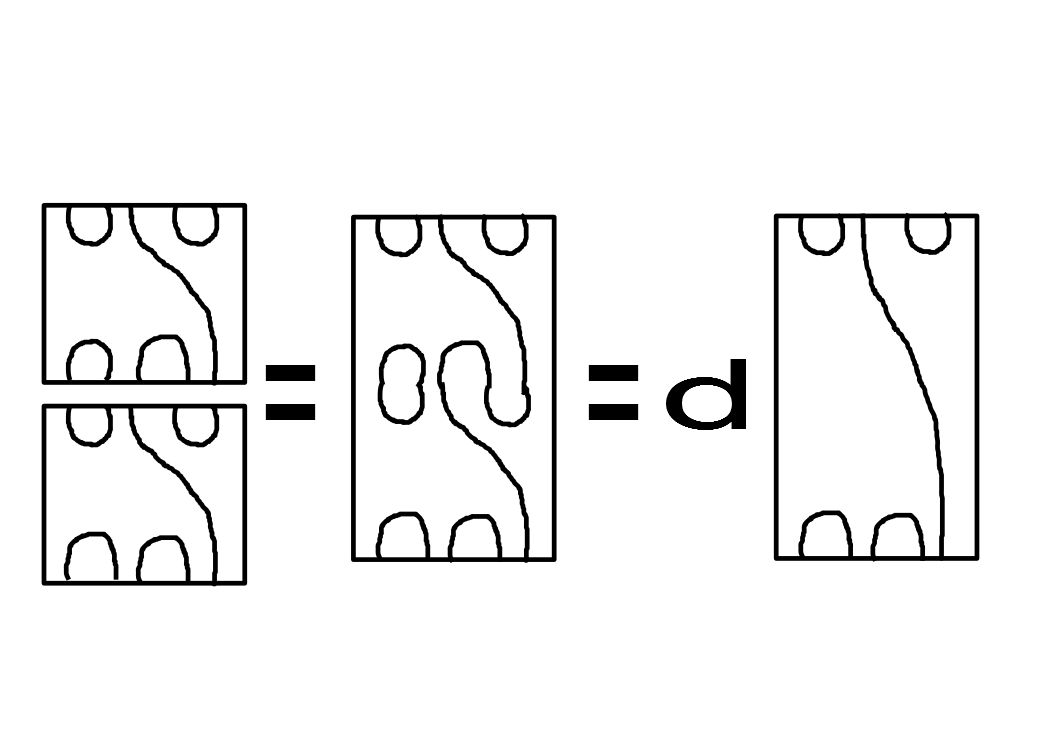
各E_iは

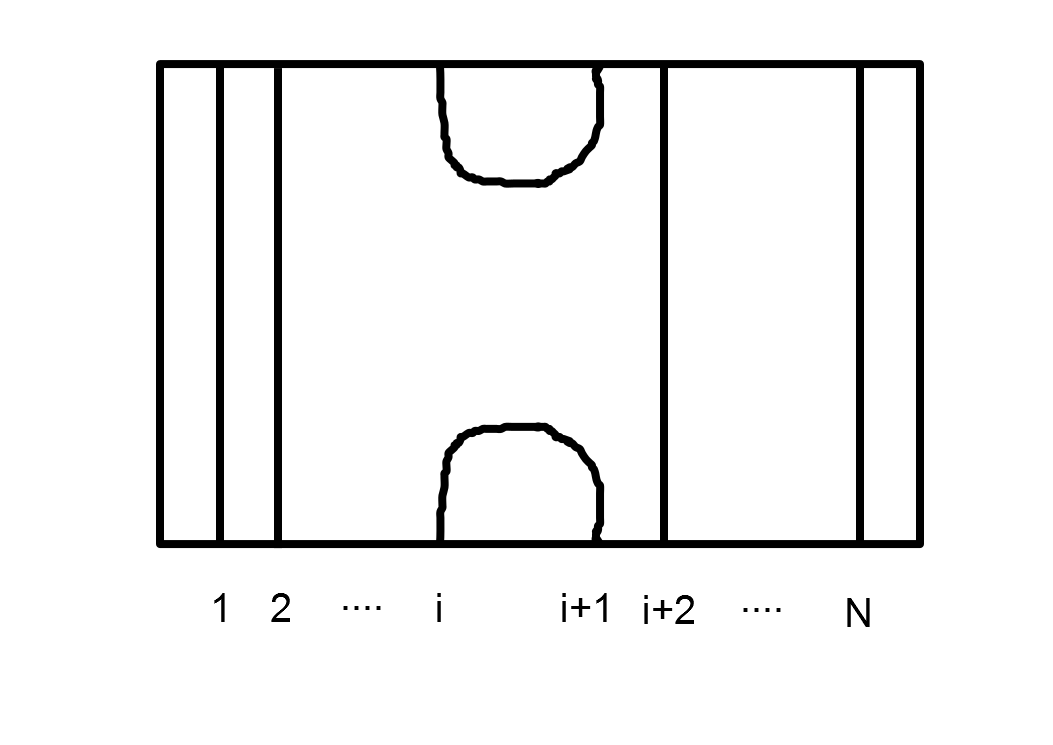
と定義されます。このような、四角のなかに紐を書いた図をKaufman n-diagramといいます。

Kaufman n-diagramに対し、次のような、Traceを定義できます。これをMarkov traceと呼びます。

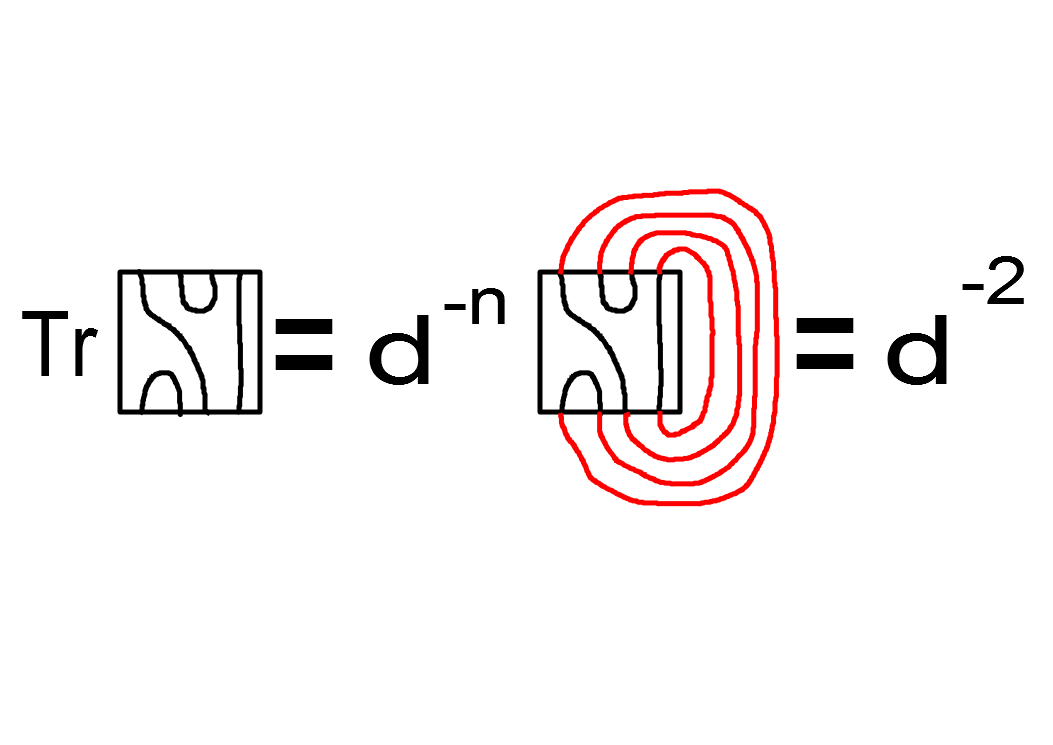
これは、次の３つの式をみたすことが簡単に示せます。

Tr(1)=1

Tr(XY)=Tr(YX)

Tr(XE_{n-1})=Tr(X)/d, where X is an element of TL_{n-1}(d)

逆に、この３つを満たす関数は、TL_n(d)内で一意に決まることが示せます。

Braid groupからTL algebraへのMap (Jones representation)を次のように定義します。

b_i → A E_i+A^{-1} I

ここで、d=−A^2−A^{-2}です。E_iがエルミートかつ|A|=1ならば、これはユニタリ表現になります。

Path-model representation

N個の頂点からなる１次元グラフを考えます。そこのPathをpとします。pは、右に行くとき０、左に行くとき１、とすれば、Binaryで表すことができます。

pを正規直交基底とするヒルベルト空間を考えます。このようなのをpath-model representationと呼びます。

このヒルベルト空間において、E_iの表現をΦ_iとすると、以下のような演算子になります。

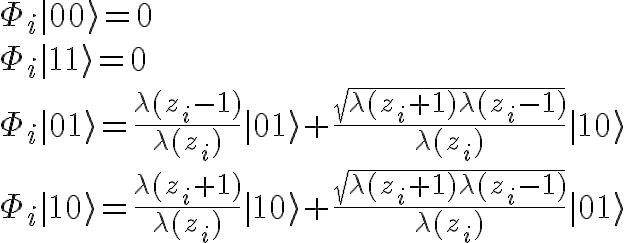
ただし、z_iはPath pのi-1 stepまで終わったときの、Graph上での位置であり、

λ(x)=sin(πx/k)

d=2cos(π/k)

です。直接計算すれば、Φ_iたちが、TL algebraのE_iたちの関係を満たしていることを確認できます。

この表現において、Tr_nを

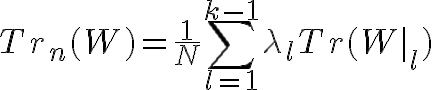
と定義します。ここで、W|_lは、Wの、H_{n,k,l}への制限、H_{n,k,l}はサイトlが最終ゴールであるようなPathのみで張られる

ヒルベルト空間、

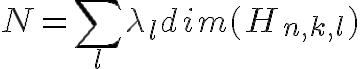
です。

すると、Tr_nは上に出てきたトレースの３つの性質を満たすことが示せます。なので、これは

TL_n(d)におけるトレースになっています。

Hadamard testによるJones polynomialの量子計算

あるユニタリUとある状態|ψ>に対し、<ψ|U|ψ>を計算したいとき、次にようにすればできます。

まず、|0>|ψ>を用意します。次に、第一レジスタにHadamard gateをかけ、そのあと、全体にControled-Uをかけます。

すると、|0>|ψ>+|1>U|ψ>を得ます。第一レジスタをXで測定すると、その平均はRe<ψ|U|ψ>になります。

Yで測定すれば、その平均はIm<ψ|U|ψ>になります。こうして、のぞみの<ψ|U|ψ>が得られます。これをHadamard testといいます。

アルゴリズム

さて、具体的にアルゴリズムを考えましょう。あるn-strands m-crossing Braid Bが与えられたとします。これのplat closure

をとったときのリンクLの、Jones多項式の

A^{-4}=exp(2π i/k)

の値を求めたいとします。

writhe は交差点の多項式で計算できるので、あとはKauffman bracket＜L＞を計算すればOKです。

Bのユニタリ表現Φ（B）をつくります。これは、まずBをb_iたちの積で書き、各b_iをユニタリ表現Φ（b_i）すればよいです。

crossingの数がmなのでこれはmステップでできます。あとは、Hadamard testにより<α|Φ(B)|α>を計算すればOKです。

ここで、|α>=|010101...>です。

trace closureの場合、確率λ_lでpを発生させ、 Hadamard testにより<p|Φ(B)|p>を計算して平均をとればOKです。

Four-step encoding

Path-model representationにおいて、

|0>=|1→2→1→2→1>

|1>=|1→2→3→2→1>

とエンコードします。このエンコーディングでユニタリを書くと、任意の２キュービットゲートは

8-strand braidで表せまず。

Fibonacci representation

Path model representationのk=5の特別な場合、Fibonacci representationというものがあります。

これは、(準備中)

The one clean qubit model of quantum computation

これは、次のような量子計算モデルです。まず１キュービットPure状態|0><0|と、

NキュービットのCompletely mixed状態I/2^Nのテンソル積状態を用意します。で、全体にユニタリをかけます。

最後に、１キュービットを測定します。Universal量子計算モデルよりはStrictに弱いけども古典では大変なある問題を

効率よく解けると信じられています。

The multivariate Tutte polynomial

G=(V,E)をグラフとし、v={v_e}を各辺に割り当てられた変数とします。すると、The multivariate Tutte polynomialは

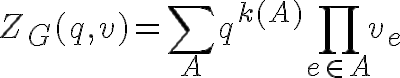
と定義されます。ここで、AはEのSubsetで、k(A)はSub graph (V,A)の中の連結な要素の数です。

Potts model

古典イジングモデルで、頂点の自由度が２ではなく一般にq（色と呼ぶ）のものであり、Nearest-neighbour interactionが、

同じ色ならJ、異なる色なら０として定義されるものです。J<0の場合、基底状態は全ての隣り合った頂点が異なる色に

なるような配置なので、温度０の分配関数は、そのような配置の数になります。

そのような、グラフを異なる色で配色する問題はNP-Completeであることが知られています。つまり、Potts modelの分配関数を

求めるのはNP-Completeな場合があるということです。

v_e=exp(β J_e)-1

とすると、Potts modelの分配関数は、Tutte polynomialになることが知られています。

Kauffman bracket of L G and the multivariate Tutte　polynomial of G

準備中

Generalized TL algebra

準備中

参考文献：

・D. Aharonov, V. F. Jones, and Z. Landau, A Polynomial Quantum Algorithm for Approximating the Jones Polynomial, Proc. 38th ACM Symp. on Theory of Computing (STOC 2006 Seattle, WA); arXiv:quant-ph/0511096

D. Aharonov and I. Arad, Polynomial quantum algorithms for additive approximations of the Potts model and other points of the Tutte plane, arXiv:quant-ph/0702008

・Dorit Aharonov and Itai Arad, The BQP-hardness of approximating the Jones polynomial, NJP 13 (2011) 035019; arXiv:0605181

Peter W. Shor, Stephen P. Jordan, Estimating Jones polynomials is a complete problem for one clean qubit, arxiv:0707.2831

G. Passante, O. Moussa, C.A. Ryan, R. Laflamme, Experimental approximation of the Jones polynomial with DQC1, PRL 103, 250501 (2009)

Raimund Marx, Amr Fahmy, Louis Kauffman, Samuel Lomonaco, Andreas Spörl, Nikolas Pomplun, John Myers, Steffen J. Glaser, NMR Quantum Calculations of the Jones Polynomial, arXiv:0909.1080